
There are several Pythagorean triples which are very well known, including: They are most useful in that they may be easily remembered and any multiple of the sides produces the same relationship. Side-basedĪll of the special side based right triangles possess angles which are not necessarily rational numbers, but whose sides are always of integer length and form a Pythagorean triple. The fact that the remaining leg AD has length follows immediately from the Pythagorean theorem. Then ABD is a 30-60-90 (Hemieq) triangle with hypotenuse of length 2, and base BD of length 1. Although the geometric proof is less apparent, it is equally trivial:ĭraw an equilateral triangle ABC with side length 2 and with point D as the midpoint of segment BC.
The proof of this fact is clear using trigonometry. The designation 30-60-90 is not only cumbersome, it references the degree, an arbitrary division of angular measure. Since this triangle is half of an equilateral triangle, some refer to this as the hemieq triangle. This is a triangle whose three angles are in the ratio, and respectively measure 30°, 60°, and 90°.

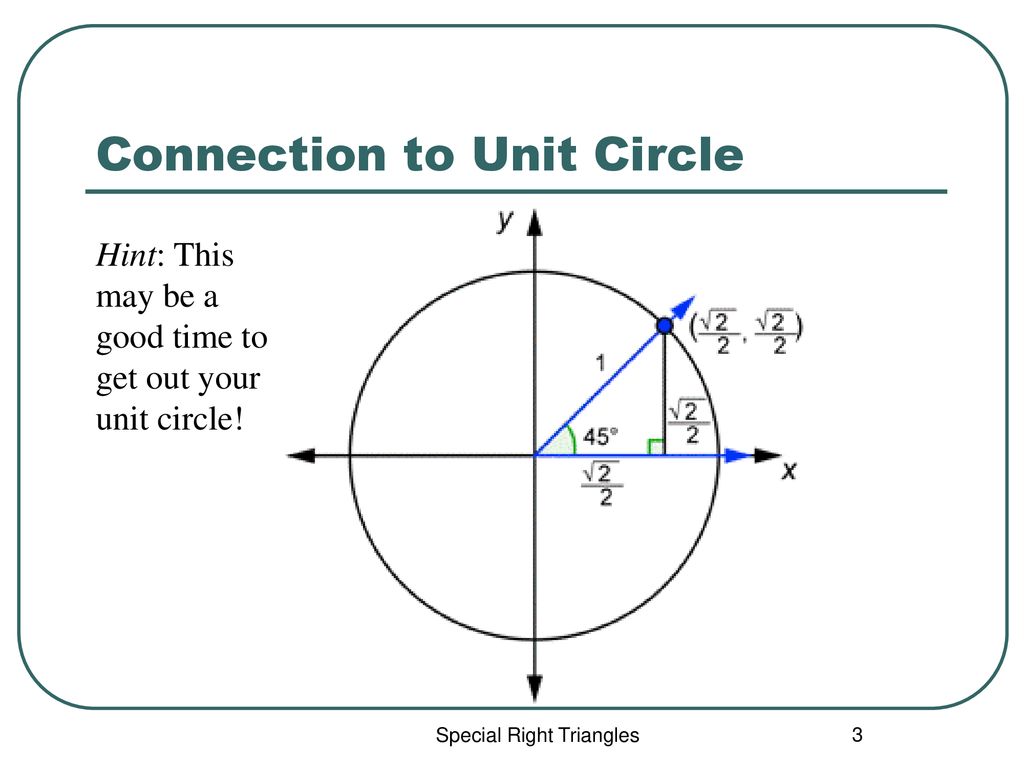
The fact that follows immediately from the Pythagorean theorem. Since two angles measure 45°, this is an isosceles triangle and we have b = 1. Say you have such a triangle with legs a and b and hypotenuse c. With the three angles adding up to 180° (π) the angles respectively measure 45° 45° and 90° The sides are in the ratioĪ simple proof.

This form is most interesting in that it may be used to rapidly reproduce the values of trigonometric functions for the angles 30°, 45°, & 60°.Ĭonstructing the diagonal of a square results in a triangle whose three angles are in the ratio. The side lengths are generally deduced from the basis of the unit circle or other geometric methods. The integer ratio of the angles of these triangles are such that the larger (right) angle equals the sum of the smaller angles. "Angle-based" special right triangles are specified by the integer ratio of the angles of which the triangle is composed. 2.3 Almost-isosceles Pythagorean triples.


 0 kommentar(er)
0 kommentar(er)
